Enfim , concluímos que o estudo das funções quadráticas é muito importante para a Física e para a Engenharia, pois descreve o movimento dos corpos sobre ação da gravidade. \ÕOO/
AGRADECEMOS A ATENÇÃO DE TODOS ! CHEGAMOS AO FIM DO NOSSO BLOG E GOSTARÍAMOS DE DESEJAR A TODOS UM FELIZ NATAL E ANO NOVO...BOAS FESTAS!!!
Sem sonhos, a vida não tem brilho. Sem metas, os sonhos não tem alicerces. E nunca esquerção :
''A vida é apenas um cálculo confuso de matemática.''
DESPEDIDA...
(B) (-2, 0)
(C) (-2, 2)
(D) (2, -2)
(E) (2, 2)
| - A única dificuldade deste exercício é achar a função escrita de um modo mais organizado. Vamos calcular o parênteses, que está ao quadrado:
- agora é só calcular o valor das coordenadas do vértice, sabendo que a=1 b=-4 e c=6.
 Resposta certa letra "E" Resposta certa letra "E" |
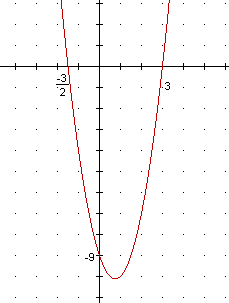 (A)
(A) (C)
(D)
(E)
- no gráfico é indicado quais são as raízes da função (-3/2 e 3), então sabemos quais são os fatores da equação (x+3/2) e (x-3). Agora efetuando a multiplicação entre estes dois fatores, achamos uma suposta equação para este gráfico:

- mas esta é somente uma suposta equação, pois veja quanto vale seu coeficiente "c". Ele vale -9/2, e no gráfico mostra que ele deve valer "-9". Então, o que devemos fazer para -9/2 virar -9? Isso mesmo, multiplicar TUDO por 2. Daí teremos a equação certa.
2x2-3x-9 Letra "C"
|
Vértice da parábola
O ponto é chamado vértice da parábola representativa da função quadrática. O conceito de vértice deriva do vocábulo latim vertex, que significa “o mais alto”. Na perspectiva da matemática, o vértice é o nome que recebe o ponto de intersecção entre os segmentos que originam um ângulo ou onde se fusiona um mínimo de três planos. A cúspide de um cone ou de uma pirâmide também se chama vértice, da mesma forma que o ponto máximo ou mínimo de uma linha curva. Na teoria dos grafos, cada vértice é considerado a unidade fundamental que compõe os grafos. Os grafos não dirigidos são compostos por vértices e arestas (isto é, pares desordenados de vértices), ao passo que os grafos dirigidos abarcam vértices e arcos (pares ordenados de vértices).
Coordenadas do Vértice y = ax² + bx + c
Ponto mínimo
Ponto máximo
Em qualquer caso, as coordenadas do vértice são dadas por:
Construção de Gráficos
Vamos partir de dois exemplos para fazermos algumas generalizações:
Exercicío Proposto
(B) intercepta o eixo horizontal em dois pontos, de abscissas negativa e positiva respectivamente
(C) intercepta o eixo das abscissas em um único ponto
(D) intercepta o eixo das abscissas em dois pontos, ambos positivos.
(E) intercepta o eixo das ordenadas em dois pontos.

 Resposta certa letra "A"
Resposta certa letra "A"Concavidade
A parábola representativa da função quadrática Y= ax2 + bx+ c pode ter a concavidade voltada para ‘cima’ ou voltada para ‘baixo’.
Exercícios Propostos
Atividade Da Pag. 150
Assistiam o video, que é referente também a esta atividade .
a)F(X)=tx² + 2x+ 5 = x é diferente do 0
B)F(X)=x²+ tx + 3 = x=IR
c)F(X)=(t - 2)x² +3 = x=IR é diferente de 2
d)F(X)= 1/t x² +2x + 5 = x é diferente do 0
e)F(X)= -5x^t + 2x + 5 = T=2
f)F(X)= (t + 1)x² + 2 = x= IR é diferente do -1
b)f(x) = 2(x-3)² ->A=2,b=-12 e C=18
c) f(x)=2(x-3)²+5 ->A=2,b=-12 e C=23
d)f(x)=(x+2)(x-3) ->A=1,b=-1 e C=-6
e) f(x)= (4x57)(3x-2) ->A=12,b=13 e C=-14
f) f(x) = (2x+3)(5x-1) ->A=10,b=13 e C= -3
Função Quadrática & Termo Independente
*Vamos Analisar o movimento de uma bola após ser chutada por um goleiro, em um tiro de meta (velocidade inicial de 72 km/h). A altura da bola varia em função do tempo. Veja a tabela a seguir.
função é completa, os coeficientes a, b e c não são nulos, e função incompleta aquela em que os
coeficientes b ou c ou ambos são nulos.
Funcão Quadrática...
Aqui está um video falando sobre a função Quadrática.Feito pela aluna Lavínia Lopes.
Obs: Não reparem os erros básicos . *FUNÇÃO QUADRÁTICA*
Comunicado...
Infelizmente ficaremos devendo a vocês a surpresa que seria um vídeo da paródia da função afim. Mas não se preocupem nesta 4 unidade terá muitas novidades e assuntos novos. Aguadem...=)
Exercício
Função
constante
- Outro
exemplo que podemos dar f(x) = b sendo a = 0,
- ex.: f(x) = 3
Exercício de Fixação
1- Esboçe o gráfico da função F(x)= 3x-4 Para fazer este gráfico, você primeiramente deve reconhecer o valor de x e y, o qual dado na função o ponto 3 corresponde a reta x e o -4 corresponde a reta y. Para isso, atribua qualquer valor a x e resolva a função. F(x)= 3x-4 F(2)= 3*2-4 F(2)=6-4 F(2)=2 Nesse caso, atribui qualquer valor a x e resolvi a equação, fazerei isto novamente a seguir: F(3)=3*3-4 F(3)=9-4 F(3)=5 Para um melhor entendimento, suponho que faça uma tabela e coloque os valores de x e de f(x), desse modo:INTRODUÇÃO
A partir de agora, vamos conhecer algumas das diferentes aplicações da Função Afim.
Durante nosso estudo, faremos exercícios contextualizados cujo principal objetivo é mostrar a
importância de estudar esse assunto indispensável do currículo escolar. Como podem observar tem exercícios logo abaixo pra que vocês tenham um entendimento melhor entre outros que postaremos em breve. A Função Afim encontra-se presente em vários ramos da ciência como, por exemplo, na Medicina, na Geologia, nas Engenharias, na Música, na Economia, na Matemática Financeira, na Física etc.
Além de mostrar sua importância, durante as tarefas propostas, o aluno deverá desenvolver parte das soluções através do uso de vídeo aulas entre outras coisas que é ''surpresa''. Já estamos desenvolvendo está surpresa que postaremos em breve .
Essas ferramentas, além de funcionarem como uma nova forma de aprender, servem como um incentivo ao estudo, pois trás para sala de aula o computador, “amigo inseparável” da maioria de nós alunos.
* Exercícios Propostos
a) Escreva a lei da função que fornece o custo total de x peças.
Largura=1,5 cm ; Perímetro = 13 cm;
Largura= 2 cm ; Perímetro = 14 cm ;
Largura = 3 cm; Perímetro = 16 cm;
Largura = 4 cm ; Perímetro = 18 cm.
R= Largura (cm) Perímetro (cm)
1 12
1,5 13
2 14
3 16
4 18
P = 2C + 2L; para C = comprimento e L = largura.
a) Largura = 1cm:
P = 2.5 + 2.1
P = 10 + 2
P = 12 cm
b) Largura = 1,5 cm
P = 2.5+2.1,5
P = 10 + 3
P = 13
c) Largura = 2cm
P = 2.5 + 2.2
P = 10 + 4
P = 14
d) Largura = 3cm
P = 2.5 + 2.3
P = 10 + 6
P = 16
e) Largura = 4cm
P = 2.5 + 2.4
P = 10 + 8
P = 18
Função : f(p) = 10 + 2y
Questão 11 - O preço do aluguel de um carro popular é dado pela tabela abaixo.
f(x) = 50 + 0,37x
50 é fixo, você escreve 50 + o que excede, o que resulta em 0,37 por km excedente = 0,37. x.
se ele não exceder, será x = 0, então ele pagará:
f(0) = 50 + 0,37.0 = 50 apenas a taxa fixa = 50.
os demais é o mesmo
Para 300 km:
f(x) = 63 + 0,37x
Para 500km:
f(x) = 75 + 0,37x
R= A taxa de variaçao é de 20 de uma funçao para outra
Questão 12- Uma pessoa vai escolher um plano de saúde entre duas opções A e B.
• O plano A cobra R$100,00 de inscrição e R$50,00 por consulta num certo período.
• O plano B cobra R$180,00 de inscrição e R$40,00 por consulta no mesmo período.
.o gasto total de cada plano é dado em função do numero x de consultas determine:
a) A equação da função correspondente a cada plano
R= A(x)=50x + 100; B(x)=40x + 180
b) Em que condições é possível afirmar que: o plano A é
mais econômico; o B é mais econômico; os dois são
equivalentes.
R= Com 8 consultas A=B, A passa a ser
mais econônico que B quando são feitas mais de 8 .
Questão 13 - Após a correção das provas de uma classe, um professor resolveu mudar o sistema de pontuação, de modo que a nota máxima continuasse 100, mas a média das notas, que havia sido 60, passou a ser 80 e que a variação das notas da antiga para a nova pontuação representa uma função afim.
a) Determine a sentença que permite estabelecer a mudança.
(100, 100)
( 60, 80)
Logo a equação é
y – 80 = (100-80)/(100-60) ( x-60)
y – 80 = 20/40 (x-60)
y – 80 = 1/2 x -30
y = 1/2 x + 50
Ou, segundo sua notação, f(x) = 1/2 P + 50
B. Se antes a nota mínima de aprovação era 50, qual é na nova pontuação?
R= P = 1/2 (50) + 50 = 75
Questão 14 -
(FGV-SP) Os gastos de consumo (C) de uma família e sua renda (X) são tais que C = 2.000 + 0,8X. Podemos então afirmar:
A funçao que representa o valor a ser pago apos um desconto de 3% sobre o valor x de uma mercadoria é?
a)f(x)=x-3
b)f(x)=0,97x
c)f(x)=1,3x
d)f(x)=-3x
e)f(x)=1,03x
Questão 16 - Sabe-se que 100g de lentilha seca contêm 26g de proteína e 100g de soja seca contêm 35g de proteína. Para um consumo diário de 70g de proteína, baseado somente no consumo de soja e lentilha:
a) quantos gramas de lentilha devem ser consumidos se for consumido 1,8g de soja?
R= 1,8g soja x 0,35 = 0,63g de proteína
Para ter um consumo de 70g de proteína, desconta o que já foi consumido em soja (70 - 0,63 = 69,37g). Precisa de 69,37g de proteína na lentilha.
A lentilha tem apenas 26% de proteína, então:
69,37g ----------------- 26%
x ------------------------- 100%
x = 266,81g de lentilha deverão ser consumidos para ter 69,37g de proteína.
b) quantos gramas de soja devem ser consumidos se for consumido 1,8g de lentilha?
R= 1,8g lentilha x 0,26 = 0,468g de proteína
70 - 0,468 = 69,532g de proteína de soja
69,532g ---------------------------- 35%
x -------------------------------------- 100%
x = 198,66g de soja deverão ser consumidos para ter 69,532g de proteína.
c) se o grama de lentilha custa R$ 0,07 e o grama de soja custa R$ 0,09, em qual das situações gasta-se menos?
Resultados da questão "a":
266,81 x 0,07 = 18,6767
1,8 x 0,09 = 0,162
Preço total = 18,6767 + 0,162 = 18,8387
Resultados da questão "b":
69,532 x 0,09 = 6,25788
1,8 x 0,07 = 0,126
Preço total = 6,25788 + 0,126 = 6,38388
Gasta-se menos na situação "B".
Questão 17 - Um casal de namorados marca um encontro numa ciclovia;ele vem do norte e ela do sul. O rapaz pedala a uma velocidade de 32 km/h e a moça pedala a 24 km/h. No instante em que a distancia entre eles é de 28 km, uma abelha, que voa a 20 km/h, parte de um ponto entre os dois até encontrar um deles; então ela volta em direção ao outro e continua nesse vaivém até morrer prensada pelas rodas das bicicletas no momento em que o casal se encontra. Quantos quilômetros voou a abelha?
R= A velocidade dela é de 20 km/h
Ela tem que percorrer em 0,5 h
x = vt (velocidade constante)
x = 20*0,5 = 10 km
A abelha voa 10 km
Questão 18 - um grande poluente produzido pela queima de combustiveis fosseis é o dióxido sulfídrico (so²). uma pesquisa feita em Oslo, noruega, demonstrou que o numero N() aproximado de peixes mortos em um certo rio por semana. é dado por uma função afim da concentração C de SO² foram feitas as seguintes medidas concentracão em pg/m³ mortes
401 106
500 109
qual é a concentração maxima de SO² que pode ser despejada no rio para que o numero de mortes não ultrapassa 15, fato que poderia prejudicar a reprodução da especie?
R= É necessário fazer mais medidas para se obter uma curva que melhor caracterize o comportamento da concentração SO² sobre a morte dos peixes, pois fazendo-se uma aproximação linear teremos a equação da reta num plano cartesiano N x C:
N(C) = a C + b
N = 3/99 C + b
N = C/33 + b
Substituindo N por 109 e C por 500, encontramos b = 109 - 15,15 = 93,85
N = C/33 + b
N(C) = C/33 + 93,85 ---> Equação da reta.
Com essa equação, mesmo que a concentração de SO² fosse zero, ainda assim teríamos aprox. a morte de 94 peixes.
Questão 19 - Devido a um desgaste, o valor (v) de uma mercadoria decresce com o tempo (t).?Por isso a desvalorização que o preço dessa mercadoria sofre em razão do tempo de uso é chamada de depreciação. A função depreciação pode ser uma função afim, como neste caso: o valor de uma máquina hoje é R$ 1000,00, e estima-se que daqui 5 anos será R$ 250,00.
a) Qual é o valor dessa máquina em t anos?
R = Segundo o exemplo dado no próprio enunciado, vamos, primeiramente, definir os valores de "a" e de "b".
I) 1000 = a * 0 + b (para t = 0)
II) 250 = a * 5 + b (para t = 5)
Calculando I, vamos obter b = 1000. Jogando o valor de "b" na equação II, vamos obter:
250 = 5a + 1000
250 - 1000 = 5a
- 750 = 5a
a = - 150
Portanto, a função é do tipo
f(t) = -150t + 1000
b) Qual será o valor dessa máquina em 6 anos?
R= Utilizando a função calculada anteriormente, vem:
f(6) = 6 * ( - 150) + 1000
f(6) = - 900 + 1000
f(6) = 100
c) Qual será sua depreciação total desse periodo de 6 anos?
R= Se o valor da mercadoria, 6 anos antes, valia R$ 1000,00 e agora vale R$ 100,00, então o valor total da depreciação será tal que:
1000 - y = 100 => y = 900


























