Matemática

DESPEDIDA...

Postado por ₪ 'Lανíίђ Loopes |

Enfim , concluímos que o estudo das funções quadráticas é muito importante para a Física e para a Engenharia, pois descreve o movimento dos corpos sobre ação da gravidade. \ÕOO/
AGRADECEMOS A ATENÇÃO DE TODOS ! CHEGAMOS AO FIM DO NOSSO BLOG E GOSTARÍAMOS DE DESEJAR A TODOS UM FELIZ NATAL E ANO NOVO...BOAS FESTAS!!!
Sem sonhos, a vida não tem brilho. Sem metas, os sonhos não tem alicerces. E nunca esquerção :
''A vida é apenas um cálculo confuso de matemática.''

Obs: Para ver o resto das publicações e o video da fução quadrática é só apertar ''POSTAGENS MAIS ANTIGAS''

Read User's Comments(0)

Postado por ₪ 'Lανíίђ Loopes |

Exercício Proposto

O gráfico cartesiano abaixo representa uma função g(x) = 2x2 + kx + m, em que k e m são números reais..

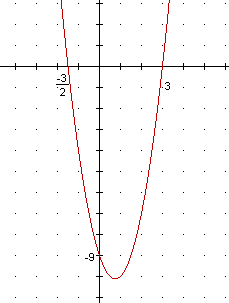Alternativas: A)-26 B)-14 C)-12 D)-08 E)-06

Resolução m = -14 xV = (x' + x'')/2 = - b/2a (-1 + 7)/2 = - k/2.2 3 = -k/4 k = -12

Alternativa C é a correta.

3)O vértice da parábola que corresponde à função $formdata=y=(x-2)^2+2$ é

(A) (-2, -2)
(B) (-2, 0)
(C) (-2, 2)
(D) (2, -2)
(E) (2, 2)

- A única dificuldade deste exercício é achar a função escrita de um modo mais organizado. Vamos calcular o parênteses, que está ao quadrado:

- agora é só calcular o valor das coordenadas do vértice, sabendo que a=1 b=-4 e c=6.

Resposta certa letra "E"

4) Qual a função que representa o gráfico seguinte?

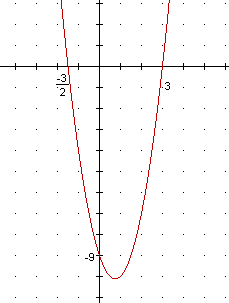(A) $formdata=y=2x^2+3x-9$

(B) $formdata=y=-2x^2+3x-9$
(C) $formdata=y=2x^2-3x-9$
(D) $formdata=y=-2x^2-3x-9$
(E) $formdata=y=2x^2+3x+9$

- no gráfico é indicado quais são as raízes da função (-3/2 e 3), então sabemos quais são os fatores da equação (x+3/2) e (x-3). Agora efetuando a multiplicação entre estes dois fatores, achamos uma suposta equação para este gráfico:

- mas esta é somente uma suposta equação, pois veja quanto vale seu coeficiente "c". Ele vale -9/2, e no gráfico mostra que ele deve valer "-9". Então, o que devemos fazer para -9/2 virar -9? Isso mesmo, multiplicar TUDO por 2. Daí teremos a equação certa.

2x²-3x-9 Letra "C"

Read User's Comments(0)

Postado por ₪ 'Lανíίђ Loopes |

Vértice da parábola

O ponto é chamado vértice da parábola representativa da função quadrática.

O conceito de vértice deriva do vocábulo latim vertex, que significa “o mais alto”. Na perspectiva da matemática, o vértice é o nome que recebe o ponto de intersecção entre os segmentos que originam um ângulo ou onde se fusiona um mínimo de três planos. A cúspide de um cone ou de uma pirâmide também se chama vértice, da mesma forma que o ponto máximo ou mínimo de uma linha curva. Na teoria dos grafos, cada vértice é considerado a unidade fundamental que compõe os grafos. Os grafos não dirigidos são compostos por vértices e arestas (isto é, pares desordenados de vértices), ao passo que os grafos dirigidos abarcam vértices e arcos (pares ordenados de vértices).

Coordenadas do Vértice y = ax² + bx + c

Ponto mínimo

Ponto máximo

Em qualquer caso, as coordenadas do vértice são dadas por:

Read User's Comments(0)

Construção de Gráficos

Postado por ₪ 'Lανíίђ Loopes |

Vamos partir de dois exemplos para fazermos algumas generalizações:

Exemplo 1 : y = f(x) = x² - 4x + 3 0 3 8 4 -1 2 0 1 3 0 8 -1 Y X

Exemplo 2 : y = f(x) = -x² + 4 0 2 -5 3 3 1 4 0 3 -1 0 -2 Y X

Read User's Comments(0)

Postado por ₪ 'Lανíίђ Loopes |

Exercício proposto

Usando fatorações, determine os zeros das seguintes funções quadráticas:

a)f(x)=x²-9 x=3 e x=-3

b)f(x)=x²-2x+1x=1(zero duplo)

c)f(x)=(x-1)²-9 x=4 e x=-2

d)f(x)=x²+6x x=0 e x=-6

e)f(x0=x²+6x+9 x= -3(zero duplo)

f)f(x)=(x+4)²-1 x= -3 e x= -5

Pagina 158

Faça completamento de quadrado em:

a)x²-2x; (x-1)²-1

b)x²+6x-16 (x+3)²-35

Usando o completamento de quadrado, determine os zeros das seguintes funções quadráticas:

a)f(x)=x²-6x+5 zeros da função 5 e 1

b)f(x)=x²+10x+21 zeros da função -3e-7

c)f(x)=x²-2x-3 zeros da função 3 e -1

d)f(x)=x²+4x+3 zeros da função -1 e -3

e)f(x)=x@-8x+12 zeros da função 6 e 2

f)f(x)=3x2-8x-3 zeros da função e -1/3

Pagina 159

Escreva na forma canônica as seguintes funções quadráticas:

a)f(x)=x²+2x-3 (x+1)2-4

b)f(x)=2x²+8x-52(x+2)2-13

c)f(x)=-x²+6x+7-(x-3)2+16

d)f(x)=x²+2x-24(x+1)2-25

e)f(x)=10+5x-5x² -5[x-1/2]2+45/4

f)f(x)=-2x²+5x-1 -2[x-5/4]2+17/8

Pagina 162

Determine, se existirem, os zeros das funções quadráticas usando a forma canônica

a) F(x) = x²-x-2 zeros da função 2 e -1

b) F(x) = 3x² + x-2 zeros da função 2/3 e -1

c) F(x) = x²-2x + 1 zeros da funçao 1

Determine, se existirem os zeros das funções quadráticas usando a fórmula:

a) F(x)= x²-3x zeros da função 3 e 0

b) F(x)= x²+4x+5 não há zeros reais

c) F(x)= -x²+2x +8 zeros da função -2 e 4

d) F(x)= x²+10x +25 zeros da função -5 (duplo)

Para que valores de m a função f(x)= (m-1)x² – 4x -1 não admite zeros reais?

M £ R tal que m <-3

Para que valores reais de k a função f(x)= kx²- 6x+1 admite zeros reais e diferentes?

K<9 e k≠0

Para que valores de m a função f(x)=(m-2)x²-2x+6 admite zeros reais?

M< 13/6 e m ≠ 2

Determine o valor de k para que a equação x²-(k+1)x + (10+k)=0 tenha uma ao dobro da outra

K=8 e k=-11/2

Use a forma canônica e determine o menor valor que a função f(x)= 2x²- 3x+4 pode assumir para todo x £ R

23/8

Qual é o maior valor da função f(x)= -3x² –x +1 pode assumir para qualquer x £ R

13/12

Determine o valor de m para que a função f(x)= 4x² -4x-m tenha zero real duplo .

M=-1

Página 179

Determine o vértice v da parábola que representa a função quadrática:

a) F(x)= x²-2x-3 v(1,-4)

b) F(x)= -x²+3x-5 v

c) F(x)= x²-4x+3 v (2,-1)

Verifique se as seguintes funções admitem valor Maximo ou valor minimo e calcule esse valor:

a) F(x)=-3x²+2x valor máximo= 1/3

b) F(x)= 2x²-3x-2 valor mínimo= -25/8

c) F(x)= -4x²+4x-1 valor Maximo=0

Determine o valor de k para que a função f(x)=(2-k) x²-5x+3. Admita valor Maximo

k>2

Qual o valor de m para que a função f(x)= (4m+1)x²-x+6

M > -1/4

Para que o valor de k o valor mínimo da função f(x)= x²-6x+3k é 3?

K=4

Determine m de modo que o valor máximo da função f(x)= (m+3)x²+8x-1 seja 3.

M=-7

Read User's Comments(0)

Exercicío Proposto

Postado por ₪ 'Lανíίђ Loopes |

Considere a função $formdata=f:\Re\rightarrow\Re$ , definida por $formdata=f(x)=ax^2+bx+c$ , com $formdata=a<0$ e $formdata=c>0$ . O gráfico de f

(A) não intercepta o eixo das abscissas
(B) intercepta o eixo horizontal em dois pontos, de abscissas negativa e positiva respectivamente
(C) intercepta o eixo das abscissas em um único ponto
(D) intercepta o eixo das abscissas em dois pontos, ambos positivos.
(E) intercepta o eixo das ordenadas em dois pontos.

SOLUÇÃO

- È dito que o coeficiente "a" é menor que zero, e o "c" é maior que zero. Portanto, deve ter concavidade para baixo (boca triste) e cortar o eixo Y em um ponto acima da origem. Podemos fazer um esboço gráfico da seguinte maneira:

- este é um gráfico que poderia ser da função dada. A única alternativa que bate com este gráfico é a letra "B".

- P.S.: Eixo das Abscissas é o eixo X e eixo das ordenadas é o eixo Y.

A razão entre a soma e o produto das raízes da equação $formdata=2x^2-7x+3=0$

(A) $formdata=\frac{7}{3}$

(B) $formdata=\frac{7}{2}$

(C) $formdata=\frac{3}{2}$

(D) $formdata=\frac{3}{7}$

SOLUÇÃO

- A soma vale 7/2 e o produto vale 3/2, portanto a razão entre a soma e o produto vale:(E) $formdata=\frac{2}{7}$

Resposta certa letra "A"

- Obs.: Sempre que for pedido razão de dois termos, o que vai em cima da divisão é o que foi dito primeiro, portanto ele pede a "soma" dividida pelo "produto".

Read User's Comments(0)

Concavidade

Postado por ₪ 'Lανíίђ Loopes |

A parábola representativa da função quadrática Y= ax2 + bx+ c pode ter a concavidade voltada para ‘cima’ ou voltada para ‘baixo’.

Se a>0, a concavidade da parábola está voltada para cima.

Se a<0, a concavidade parábola está voltada para baixo.

Forma canônica

A construção do gráfico da função quadrática Y=ax2 +bx+ c com o auxílio de uma tabela de valores X e Y, como foi feito o item anterior , torna-se ás vezes um trabalho impreciso, pois na tabela atribuímos a X alguns valores interiores e pode acontecer que em determinada função quadrática as valores de abscissa (valores de X), em que a parábola intercepta o eixo dos X ou abscissa do ponto da parábola de maior ou menor ordenada, não são inteiros.

Para iniciarmos um estudo analítico mais detalhado da função quadrática , vamos primeiramente transformá-la em outra forma mais conveniente, chamada forma canônica .

Zeros

Os zeros ou raízes da função quadrática f(x)=ax2 +bx+ c são os valores de X reais tais que F(x)=0 e, portanto as, soluções de equação do segundo grau ax2 + bx+ c = 0.

Utilizando a forma canônica, temos:

Números de raízes

Observe que a existência de raízes para a equação do segundo grau ax2 + bx + c = 0 fica condicionada ao fato de raiz de delta ser real . Assim, temos três a casos a considerar:

Read User's Comments(0)

Matemática

QUEM SOMOS

Archives

DESPEDIDA...

Vértice da parábola

Coordenadas do Vértice y = ax² + bx + c

Ponto mínimo

Ponto máximo

Em qualquer caso, as coordenadas do vértice são dadas por:

Construção de Gráficos

Exercicío Proposto

Concavidade